DDPM (Diffusion model) 논문
<Denoising Diffusion Probabilistic Models> 리뷰
학회 : NeurIPS 2020
저자 : Jonathan Ho, Ajay Jain, Pieter Abbeel
소속 : UC Berkeley
링크 : https://arxiv.org/pdf/2006.11239
참고하면 좋은 리뷰 : https://xoft.tistory.com/32
[개념 정리] Diffusion Model
GAN, VAE 와 같은 생성 모델(Generative Model) 중 하나로써, 2022년에 이슈가 되었던 text-to-image 모델인 Stable-Diffusion, DALL-E-2, Imagen의 기반이 되는 모델입니다. 많은 논문에서 Diffusion Model이 인용되지만 수
xoft.tistory.com
https://kimjy99.github.io/%EB%85%BC%EB%AC%B8%EB%A6%AC%EB%B7%B0/ddpm/
[논문리뷰] Denoising Diffusion Probabilistic Models (DDPM)
DDPM 논문 리뷰 (NeurIPS 2020)
kimjy99.github.io
https://jungsoo-ai-study.tistory.com/47
DDPM: Denoising Diffusion Probabilistic Models
NeurIPS 2020Denoising Diffusion Probabilistic ModelsJonathan Ho, Ajay Jain, and Pieter Abbeel본 논문은 이미지 생성 분야에서 최초로 Diffusion 방식을 제안한 연구로, 생성형 인공지능 연구에 있어 중요한 전환점을 제
jungsoo-ai-study.tistory.com
1. Abstract & Introduction
Diffusion model을 발전시킨 논문이다. Diffusion model은 Forward Process에서는 Markov Chain이 점진적으로 noise를 추가하여 최종적으로는 완전한 노이즈인 가우시안 noise를 만든다. 반대로 reverse process에서는 가우시안 noise를 제거하여 원하는 데이터에 맞는 샘플을 만든다. 즉, 데이터를 노이즈로 한 번에 만들고 한 번에 생성하는 것이 아닌 점차적으로 노이즈를 추가하고 빼는 과정을 수행하여서 선명한 결과를 얻고자 하는 생성 모델이다.
- Markov Chain : 현재 상태는 (t) 이전 상태(t-1)에만 의존한다는 특성
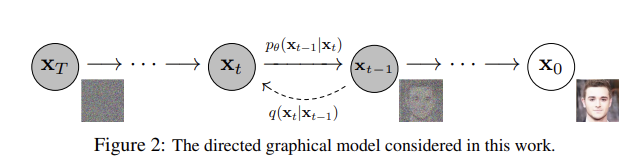
2. Background
Diffusion 모델에서는

과 같이 정의한다. x1, x2, x_T는 데이터 x0 ~ q(x0)와 같은 크기이고 다음 P를 구하는 과정을 reverse process라고 하며 최종적으로 Pt는 완전히 가우시안 분포를 따른다.
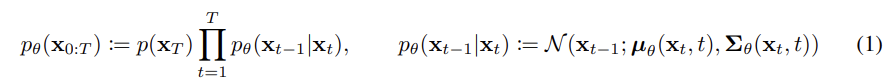
- diffusion에서 reverse process의 한 스텝에서의 분포를 '가우시안으로 가정하여서' 모델링한 결과이다. 만약 noisy한 상태 xt가 주어졌을 때 바로 이전 단계는 평균이 mu 이고 분산이 sigma인 정규 분포에서 샘플링 된다는 것을 보여준다.
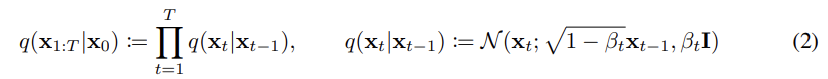
- 다음은 Forward 과정에서의 노이즈를 추가하는 방식이다. beta의 크기에 노이즈를 얼마나 추가할 지가 결정되며, beta의 값이 커질 수록 노이즈 값이 많이 추가되는 것을 알 수 있다. (beta 값은 주어진 상수)
- 확률 분포 q가 주어졌을 때 이 확룰 분포를 가장 잘 모델링하는 확률 분포 P를 찾는 문제로 변환됨.
- likelihood 정리 : http://data-scientist-brian-kim.tistory.com/91#google_vignette
- MLE 정리 : https://xoft.tistory.com/31
- 즉, 확률 분포 q에서 관측한 값으로 확률 분포 p의 likelihood를 구하였을 때, 그 likelihood 값이 최대가 되는 확률 분포를 찾는 MLE(Maximum Likelihood Estimation) 문제이다. 이때 -log를 붙이면 최소화하는 방향으로 loss를 설계할 수 있다. (NLL)
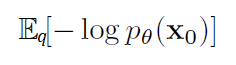
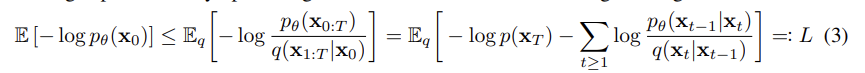
- 위 식을 이를 활용하여서 KL - divergence를 활용하면 다음과 같이 Loss 값이 정리되는 것을 확인할 수 있다.
- 다음 식 정리 구체적 과정 : https://xoft.tistory.com/33
- KL - divergence : https://hyunw.kim/blog/2017/10/27/KL_divergence.html

- 각 단계에서의 p와 q의 Cross Entropy 값을 낮추는 방향으로 나타나게 되는 것으로 해석할 수 있다.
-> 논문의 목표는 이러한 Diffusion 모델의 loss 값을 아래의 식으로 바꾸는 과정이다.

3. Diffusion Models and denoising autoencoder
3.1 Forward process and L_T

- 실험에서는 forward process의 분산 beta를 상수로 고정할 것이기 때문에 q에서는 학습되는 파라미터가 없어서 L_T는 상수이므로 무시할 수 있다. (학습할 parameter가 없어서 L_T를 Loss 값으로 사용할 수 없음)
- L0와 관련된 식은 영향력이 작아서 제거할 수 있다.
3.2 Reverse process and L1:T-1
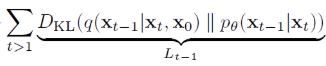
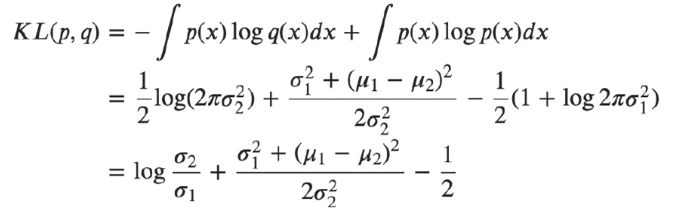
- 표준편차 값은 beta_t는 상수로 고정하기에 학습으로 바뀌지 않는 값으로 무시할 수 있다.
-> KL 값을 최소화 하는 문제는 (분산을 고정한 설정에서는) 정답의 평균과 모델의 평균이 가갑게 되도록 학습하는 문제로 변환된다.

- 아래 기호로 beta를 재정의하게 될 때

- xt 값은 아래와 같이 정리할 수 있다.
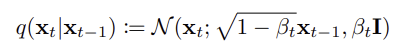

- 위의 수식을 x0으로 부터 생성하는 식으로 바꾸기 위해서는 다음의 식을 이용한다.

- 따라서 x_0로 부터 만들어지는 x_t의 값을 다음과 같이 나타낼 수 있다.
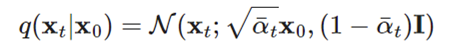
- 아래의 식으로 부터 Loss 값에 필요한 mu 값을 구할 수 있기 때문에 다음의 식으로 mu 값을 구한다.

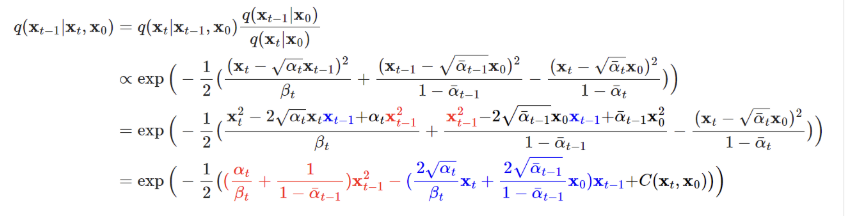
- 첫번째 줄 : 베이즈 정리 활용 https://datascienceschool.net/02%20mathematics/06.06%20%EB%B2%A0%EC%9D%B4%EC%A6%88%20%EC%A0%95%EB%A6%AC.html
- 두번째 줄 : Gaussian Distribution 식을 활용하여 나타냄

그리고 이를 Gaussian Distribution의 분산과 평균의 정의를 활용하여서 나타내면 다음과 mu와 beta 값을 정리할 수 있다.

- 추가적으로 정리하기 위해서 이전에 사용하였던 아래 식을 활용하여서 정리할 수 있다.

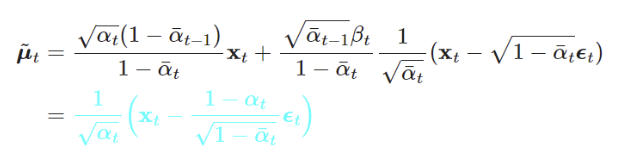
- 이를 정리 한 L_t-1의 값에 대해서 대입하게 되면 아래의 식으로 나타날 수 있다.

- Loss 값을 계산하는 것으로 weight term을 제거한다면 최종적으로 아래 수식이 나오게 되는 것을 알 수 있다.

- 따라서 다음의 과정을 통해서 Training 되며 Sampling 되는 것을 알 수 있다. Training 하면서 epsilon_theta 값을 학습함.

- Training
- epslion값은 Gaussian Distribution을 따르며 Loss 이전에 구한 식을 통해서 Epslion_theta 값을 학습한다.
- Sampling
- X_T도 Gaussian Distribution을 따르며 t-1번째의 이미지는 t번째 이미지와 학습된 Epslion_theta에 의해서 생성된다.
4. Experiments
beta_t 값에 의해서 스케쥴링이 가능하다.
DDPM에서는 beta_t 을 변화할 때에 constant, linear, quadratic scheduls로 실험했고, 다른 결과를 보였다. beta_1 = 0.0001, beta_t =0.02로 두고 linear schedule를 최종적으로 활용하였다.

- DDPM에서는 CIFAR10을 데이터 셋으로 삼아서 데이터를 학습하였다. CIFAR 데이터 셋을 가지고 Inception Score, FID score, Negative log Likelihood (NLL)을 측정하였고 DDPM이 좋은 성능을 보였다.
- Inception Score : 생성 이미지 x를 분류기에 넣어서 나오는 클래스 확률을 보고, 각 이미지가 하나의 클래스에 뚜렷하게 속하고, 전체 생성 샘플이 다양한 클래스에 고르게 포함되는지를 보는 점수 (점수 높을 수록 좋음)
- FID score : 생성 이미지와 실제 이미지를 둘 다 중간 feature 공간으로 보내서 real feature과 generated feature 분포의 거리를 재는 방식 (점수 낮을 수록 좋음)
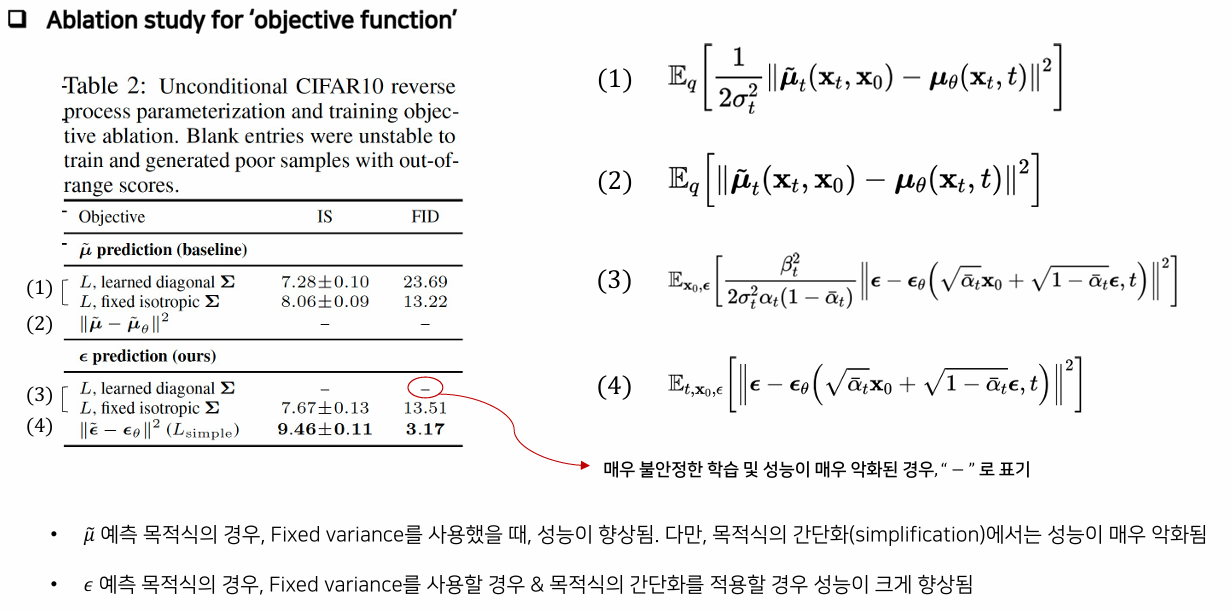
- Objective function을 loss 유도 과정에서 중간 식을 활용하였을 경우의 IS와 FID score 값
- 결과적으로 epslion을 prediction 하고 L을 simple로 한 것이 가장 성능이 좋은 것을 알 수 있다.

